Ce 14 mars célèbre la journée du nombre Pi, cette constante mathématique «qui est le rapport de la circonférence d'un cercle à la longueur de son diamètre».
Ce 14 mars célèbre la journée du nombre Pi, cette constante mathématique «qui est le rapport de la circonférence d'un cercle à la longueur de son diamètre».
Pi est appelé parfois constante d’Archimèdea, représenté par la lettre grecque du même nom (minuscule et en italique) : π.
Pourquoi aujourd'hui ? Parce que nous sommes le 3/14 (date en version us), soit 3,14..., la valeur approximative de Pi. On peut trouver une valeur approchée de π de façon empirique, en traçant un cercle, puis en mesurant son diamètre et sa circonférence, puis en divisant la circonférence par le diamètre.
Une autre approche géométrique, attribuée à Archimède, consiste à calculer le périmètre Pn d’un polygone régulier à n côtés et à mesurer le diamètre d de son cercle circonscrit, ou celui de son cercle inscrit25. Plus le nombre de côtés du polygone est grand, meilleure est la précision obtenue pour la valeur de π.
Archimède a utilisé cette approche en comparant les résultats obtenus par la formule en utilisant deux polygones réguliers ayant le même nombre de côtés, pour lesquels le cercle est pour l’un circonscrit et pour l’autre inscrit. Il a réussi, avec un polygone à 96 côtés, à déterminer que 3 + 10⁄71 < π < 3 + 1⁄7.
On peut également obtenir des valeurs approchées de π en mettant en œuvre des méthodes plus modernes. La plupart des formules utilisées pour calculer π se basent sur la trigonométrie et le calcul intégral. Cependant, certaines sont particulièrement simples, comme la formule de Leibniz :
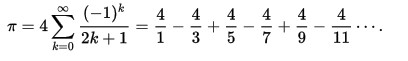
D'ailleurs, on peut toujours visiter la salle dédiée au Palais de la Découverte, à Paris, avec les 707 décimales.